Booster son patrimoine avec la puissance des intérêts composés
Albert Einstein est principalement connu pour ses travaux relatifs à la physique. En dehors de la physique, il nous a livré d'autres pépites tel que son regard sur les intérêts composés. Selon lui "les intérêts composés sont la huitième merveille du monde. Celui qui le comprend s'enrichit, celui qui ne le comprend pas, le paie". D'un coup, j'imagine que ton regard sur Albert Einstein vient de changer. Et si ton regard n'a pas changé, j'ose imaginer que tu préfères à minima te trouver du côté de ceux qui s'enrichissent plutôt que du côté de ceux qui le paie ! Pour cela, il suffit de comprendre le principe des intérêts composés et de connaitre les sept autres merveilles du monde ! Pour les autres merveilles, je te laisse faire tes recherches. En revanche, pour comprendre les intérêts composés tu es au bon endroit !
On va commencer par un petit échauffement avec une explication simple sur ce que sont les intérêts composés. Et après ce petit échauffement, on passe aux choses sérieuses ou tu auras le droit à des exemples détaillés sur ce que les intérêts composés peuvent faire pour toi ! Enfin, cela sera à toi de les utiliser, et pour cela… tu pourras parcourir les autres pages de ce site pour savoir comment investir, où investir et profiter en même temps de ce booster de patrimoine !
Que sont les intérêts composés ?
Avant de voir les intérêts composés, je vais placer ici quelques définitions très simples afin de m'assurer que toi et moi, nous parlons bien le même langage. Tout d'abord c'est quoi un intérêt ? Un intérêt est tout simplement un revenu, une rémunération que tu obtiens car tu auras prêté de l'argent. Au final, tu récupéreras l'argent prêté et aussi un bonus car tu auras prêté cet argent. Ce bonus est généralement défini en avance et prend souvent la forme d'un pourcentage. Ce pourcentage sera appliqué à la somme que tu auras prêtée. Et… tu arrives à la définition des intérêts simples. A savoir des intérêts calculés uniquement sur le montant d'un capital, sans prendre en compte les intérêts antérieurs.
Par exemple, tu prêtes 100€ à un taux de 10% sur une année. A la fin de l'année, on te rend tes 100€ et aussi la rémunération car tu as prêté cet argent, soit 10€ d'intérêts (100€x 10% = 10€). Tu as prêté 100€ et tu récupères à la fin de l'année 110€ soit un bonus brut de 10€.
Pour utiliser le principe des intérêts composés, il suffit de continuer à prêter ton capital initial (100€) et aussi les intérêts gagnés (10€). Si je reprends l'exemple, la première année tu as prêté 100€ à un taux de 10%. A la fin de l'année tu récupères 110€. Tu prêtes tes 110€ une nouvelle année et toujours à un taux de 10%. A la fin de l'année, tu récupères tes 110€ et aussi tes intérêts qui sont cette fois-ci équivalent à 11€ (110€x 10% = 11€).
La seconde année tu auras donc généré des intérêts simples sur ton capital initial, soit 100€ x 10% = 10€. Et aussi des intérêts sur des intérêts, soit 10€ x 10% = 1€. C'est ça le principe des intérêts composés ! Grâce à ce principe, tu auras gagné 1€ de plus la seconde année pour un même capital initial. En résumé, les intérêts simples sont des intérêts sur le capital. Les intérêts composés prennent en compte les intérêts sur le capital et aussi les intérêts sur les intérêts.
Comment calculer les intérêts composés ?
Je vais être honnête avec toi, si tu n'es pas curieux ou si tu es en colère avec les mathématiques, tu peux directement passer cette partie et aller directement aux exemples. Et si tu es curieux de savoir les savants calculs qui ont été utilisé pour créer les exemples que tu vas découvrir juste après… Et bien dans ce cas, je te conseille de rester encore un peu sur cette partie.
Avant de te donner la formule qui te permettra d'illuminer tes nuits de doux rêves, je vais commencer par une règle qui te permettra de faire rapidement des estimations. Cette règle s'appelle la règle du 72 ! Cela n'a rien à voir avec le fait que le 69 était déjà un nombre... déposé. Mais plutôt parce qu'avec le nombre 72 les calculs fonctionnent beaucoup mieux pour estimer le nombre d'année qu'il te faudra pour doubler la valeur de ton investissement. La formule est la suivante : Y = 72/r Dans cette formule, Y (Years) est le nombre d'année nécessaires pour doubler ton investissement. Et r est le taux d'intérêt annuel composé.
Imagine que tu décides d'investir un certain capital, une certaine somme sur un véhicule financier à 10%. En utilisant cette formule, tu peux estimer qu'il te faudra un peu plus de 7 années pour doubler le capital investi (Y = 72/10 = 7,2 années). Il s'agit d'une estimation, si tu effectues les calculs en réel tu obtiendras une légère différence. Ce qui m'amène à la formule qui te permettra d'illuminer tes rêves… A=P(1+r/n)^nt Bon, je ne sais pas si elle va réellement illumine tes rêves mais au moins tu l'auras ! Au niveau de cette formule, A représente la valeur future de ton investissement. P est le capital initial que tu auras investi. Le taux d'intérêt set représenté par r, la fréquence de capitalisation par n et t pour la durée de ton placement en années.
La fréquence de capitalisation est le nombre de fois où les intérêts seront distribués au cours d'une année. Tu te doutes bien qu'au plus ce nombre est élevé, au plus tu vas pouvoir réaliser des intérêts sur des intérêts… et donc d'optimiser l'utilisation du principe des intérêts composés. Si tu places par exemple 100€ à 10% durant 10 années, et que les intérêts sont versés une fois par an, ton capital à la fin de cet investissement ne sera plus de 100€ mais de 259€. Au niveau des formules, je pense que tu as déjà de quoi t'amuser. Il est désormais temps de passer aux exemples !
L'importance des intérêts composés au travers d'un petit exemple…
Les intérêts simples et composés me font penser au test du marshmallow que l'on fait passer à certains enfants. Il pourrait s'agir d'un test élaboré par un célèbre psychologue s'appelant Marshmallow. Où tout plus simplement car on utiliser une guimauve pour faire ce test. Je penche plutôt pour l'utilisation de la guimauve.
L'idée de ce test est de placer une guimauve (ça fonctionne aussi avec d'autres bonbons) devant un enfant. On propose un choix à l'enfant. Il peut manger de suite la guimauve. Où il peut attendre un certain temps sans toucher la guimauve. Et s'il y arrive, il aura le droit à deux guimauves.
Ce test a été réalisé pour la première fois en 1972, non pas par le psychologue Marshmallow, mais plutôt par Walter Mischel. Ok… tu vas me dire quel est le lien entre des guimauves et des intérêts simples ou composés ? Eh bien, ce test très simple permet de mesurer la sensibilité des personnes à la gratification différée. C’est-à-dire notre capacité à faire preuve de contrôle de soi, d'accepter un sacrifice dans le moment présent car on dispose d'une vision long terme qui inclut… des bénéfices futurs plus importants que les bénéfices immédiats.
Tu commences à bien comprendre où je veux en venir… Les intérêts simples représentent le bénéfice immédiat (et plus faible). Les intérêts composés représentent le bénéfice plus lointain (mais plus important !). Tu te dis certainement que ce test c'est de la guimauve… et bien 1 000 enfants ont été suivis durant les 30 années qui ont suivi ce test. Les enfants qui ont pris de suite la guimauve ont eu plus de problèmes de santé, plus d'addictions, plus de casier judiciaire et pour revenir au domaine financier… ils sont beaucoup plus nombreux à être dans une situation plus précaire que ceux qui ont attendu pour avoir plus de guimauve.
Tu connais certainement des personnes qui sautent de suite sur la première guimauve qui passe sous leurs yeux. Peut-être fais-tu parti de ces personnes ? Dans un cas comme dans l'autre, toi et moi, nous allons suivre l'exemple de deux personnes. La première personne s'appelle Guimauve et la seconde Richard (oui je sais ça casse le suspense le choix des prénoms…).
Guimauve et Richard disposent d'un même capital de départ, à savoir 5 000€. Si tu n'as pas de capital de départ et que tu veux t'en constituer un, ou si tu veux faire grossir ce capital initial plus vite, je t'invite à cliquer ici .
Nos deux personnages vont investir leur 5 000€ sur un véhicule financier à 5%. 5% ?!!! Impossible d'avoir ce genre de taux pour un investissement… Ah bon ? Si tu es septique, je t'invite à cliquer ici pour découvrir que c'est possible, que 5% c'est peu… et à faire la même chose !
La seule différence est que Guimauve va retirer chaque année ses intérêts (pour les utiliser ?). Richard laissera ses intérêts. Ce qui te permettra de comparer l'évolution du cumul des intérêts suivant un capital qui sera fixe pour Guimauve et qui va évoluer pour Richard.
| PATRIMOINE DE GUIMAUVE | PATRIMOINE DE RICHARD | |||||||
| CAPITAL | INTERETS | FIN D'ANNEE | CUMUL INTERETS | ANNEE | CAPITAL | INTERETS | FIN D'ANNEE | CUMUL INTERETS |
| 5 000 € | 250 € | 5 250 € | 250 € | 1 | 5 000 € | 250 € | 5 250 € | 250 € |
| 5 000 € | 250 € | 5 250 € | 500 € | 2 | 5 250 € | 263 € | 5 513 € | 513 € |
| 5 000 € | 250 € | 5 250 € | 750 € | 3 | 5 513 € | 276 € | 5 788 € | 788 € |
| 5 000 € | 250 € | 5 250 € | 1 000 € | 4 | 5 788 € | 289 € | 6 078 € | 1 078 € |
| 5 000 € | 250 € | 5 250 € | 1 250 € | 5 | 6 078 € | 304 € | 6 381 € | 1 381 € |
| 5 000 € | 250 € | 5 250 € | 2 500 € | 10 | 7 757 € | 388 € | 8 144 € | 3 144 € |
| 5 000 € | 250 € | 5 250 € | 5 000 € | 20 | 12 635 € | 632 € | 13 266 € | 8 266 € |
| 5 000 € | 250 € | 5 250 € | 7 500 € | 30 | 20 581 € | 1 029 € | 21 610 € | 16 610 € |
| 5 000 € | 250 € | 5 250 € | 10 000 € | 40 | 33 5241 € | 1 676 € | 35 200 € | 30 200 € |
| 5 000 € | 250 € | 5 250 € | 12 500 € | 50 | 54 607 € | 2 730 € | 57 3370 € | 52 337 € |
Tu retrouves au milieu le nombre d'années écoulées. De chaque côté, le capital initial au démarrage de l'année en question, les intérêts sur ce capital en prenant un taux de 5%, la somme que cela représente en fin d'année (capital + intérêts) et enfin la somme que représente les intérêts seuls au fur et à mesure des années…
Puisque Guimauve retire chaque année ses intérêts, le capital au démarrage de chaque année est constant. Puisque Richard laisse chaque année ses intérêts, le capital au démarrage de chaque année comporte le capital augmenté des intérêts générés précédemment. La colonne cumul intérêts te permet de te rendre compte de l'écart qui se creuse entre une personne qui ne récupère que des intérêts simples, contre celle qui se sert du principe des intérêts composés (et remet à plus tard la récupération de la guimauve !) Tu pourras également voir ci-dessous la représentation entre le cumul des intérêts simples et le cumul utilisant le principe des intérêts composés.
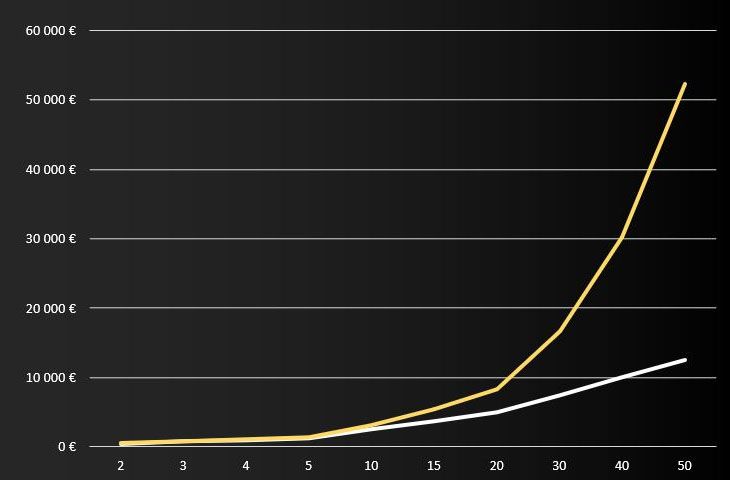
Comme tu peux le voir, l'écart est peu important au début. Puis il se creuse rapidement et devient de plus en plus important au fur et à mesure que le temps passe. Ce qui est normal, puisque le capital de Richard ne fait que grossir année après année. Ceci génère de plus en plus d'intérêts sur des intérêts sur des intérêts sur… bon tu as compris quoi. Le capital de départ, le temps et également le taux jouent tous un rôle important dans l'évolution de cet écart. Si je reprends les mêmes données de départ en changeant simplement le taux qui passe de 5% à 10% pour Guimauve et Richard. Les nouvelles données seraient les suivantes :
| PATRIMOINE DE GUIMAUVE | PATRIMOINE DE RICHARD | |||||||
| CAPITAL | INTERETS | FIN D'ANNEE | CUMUL INTERETS | ANNEE | CAPITAL | INTERETS | FIN D'ANNEE | CUMUL INTERETS |
| 5 000 € | 500 € | 5 500 € | 500 € | 1 | 5 000 € | 500 € | 5 500 € | 500€ |
| 5 500 € | 500 € | 5 500 € | 1 000 € | 2 | 5 500 € | 550 € | 6 050 € | 1 050€ |
| 5 000 € | 500 € | 5 500 € | 1 500 € | 3 | 6 050 € | 605 € | 6 655 € | 1 655 € |
| 5 000 € | 500 € | 5 500 € | 2 000 € | 4 | 6 655 € | 666 € | 7 321 € | 2 321 € |
| 5 000 € | 500 € | 5 500 € | 2 500 € | 5 | 7 321 € | 732 € | 8 053 € | 3 053 € |
| 5 000 € | 500 € | 5 500 € | 5 000 € | 10 | 11 790 € | 1 179 € | 12 969 € | 7 969 € |
| 5 000 € | 500 € | 5 500 € | 10 000 € | 20 | 30 580 € | 3 058 € | 33 637 € | 28 637 € |
| 5 000 € | 500 € | 5 500 € | 15 000 € | 30 | 79 315 € | 7 932 € | 87 247 € | 82 247 € |
| 5 000 € | 500 € | 5 500 € | 20 000 € | 40 | 205 724 € | 20 572 € | 226 296 € | 221 296 € |
| 5 000 € | 500 € | 5 500 € | 25 000 € | 50 | 533 595 € | 53 359 € | 586 954 € | 581 954 € |
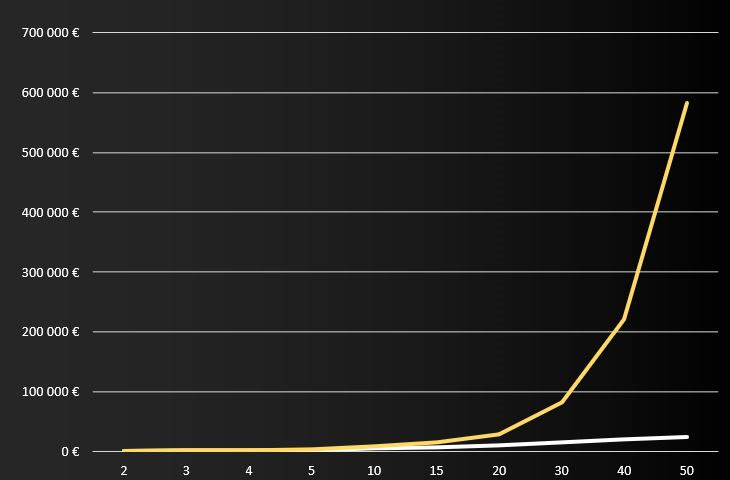
Comme tu peux t'en rendre compte, il est parfois intéressant de laisser trainer la guimauve sur la table… Maintenant que le principe est certainement plus clair pour toi, je te propose de voir une application encore un peu plus concrète de ce fameux principe des intérêts composés…
Le principe des intérêts composés appliqué au Compte Titres Ordinaire et au Plan d'Epargne en Actions
Il existe trois enveloppes afin d'investir ton capital en bourse. Il s'agit du Compte-Titres Ordinaire (CTO) , du Plan d'Epargne en Actions (PEA) et de l' Assurance Vie (AV) . Tu pourras retrouver plus d'informations sur ces enveloppes en cliquant sur les liens précédents.
J'aurai pu faire un comparatif entre l' AV et le CTO également. L'idée ici est que les gains réalisés et qui restent à l'intérieur d'un PEA (ou d'une AV ) ne sont pas imposées tant qu'ils restent à l'intérieur du périmètre du PEA (ou de l' AV ). Pour le CTO , les gains sont imposés chaque année au travers du Prélèvement Forfaitaire Unique (PFU), encore appelé Flat Tax, et qui s'élève à 30%.
Au lieu de comparer le patrimoine de Guimauve et de Richard, cette fois-ci je vais comparer un même capital placé sur un CTO ou sur un PEA . Afin de simplifier le tout, je ne vais pas incorporer les frais relatifs aux placements qui seront effectués. Et chaque placement durera une année. Le capital initial sera de 5 000 €, le taux sera de 10% et 30% de PFU seront appliqués sur les gains pour le patrimoine en CTO .
| PATRIMOINE CTO | PATRIMOINE PEA | |||||
| CAPITAL | INTERETS | CUMUL (-PFU) | ANNEE | CAPITAL | INTERETS | CUMUL |
| 5 000 € | 500 € | 5 350 € | 1 | 5 000 € | 500 € | 5 500 € |
| 5 350 € | 535 € | 5 725 € | 2 | 5 500 € | 550 € | 6 050 € |
| 5 725 € | 572 € | 6 125 € | 3 | 6 050 € | 605 € | 6 655 € |
| 6 125 € | 613 € | 6 554 € | 4 | 6 655 € | 666 € | 7 321 € |
| 6 554 € | 655 € | 7 013 € | 5 | 7 321 € | 732 € | 8 053 € |
| 9 192 € | 919 € | 9 836 € | 10 | 11 790 € | 1 179 € | 12 969 € |
| 18 083 € | 1 808 € | 19 348 € | 20 | 30 580 € | 3 058 € | 33 637 € |
| 35 571 € | 3 557 € | 38 061 € | 30 | 79 315 € | 7 932 € | 87 247 € |
| 69 974 € | 6 997 € | 74 872 € | 40 | 205 724 € | 20 572 € | 226 296 € |
| 137 650 € | 13 765 € | 147 285 € | 40 | 533 595 € | 53 359 € | 586 954 € |
Comme tu peux le voir, le capital au démarrage de chaque année augmente. Le principe des intérêts composés est appliqué au CTO et au PEA. La principale différence ici est la fiscalité qui n'est pas la même entre le CTO et le PEA. Les gains du CTO sont taxés au travers du Prélèvement Forfaitaire Unique (PFU) à hauteur de 30%.
Si tu prends la fin de la première année, un capital de 5 000€ placé à 10% rapportera 500€ en intérêt. En CTO, les gains seront soumis au PFU, soit 500€ x 30% = 150€ d'imposition. 500€ de gain - 150€ d'imposition, il restera 350€ que je vais pouvoir ajouter au capital initial, soit 5 350€ dans le cadre du CTO pour démarrer la seconde année. En PEA, les gains ne sont pas imposés tant que tu restes dans le périmètre du PEA. C'est la raison pour laquelle le capital au démarrage de la seconde année est de 5 500€ et non de 5 350€, car il n'y a pas eu cette imposition de 150€… Tu pourras te faire une idée de l'impact du PFU en comparant les colonnes CUMUL ou en regardant la représentation graphique ci-dessous :
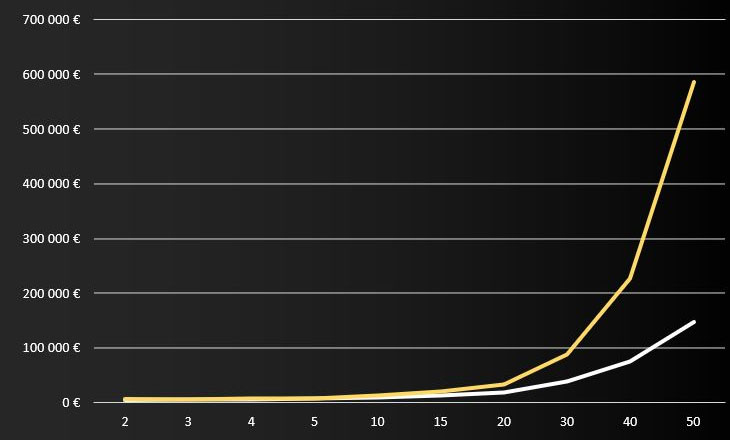
Est-il préférable d'aller sur un Plan d'Epargne en Actions (PEA) plutôt qu'un Compte-Titres Ordinaire (CTO) au regard de cette conclusion ? Et bien tout dépend de tes objectifs et de la stratégie que tu as mise en place pour les atteindre. Pour pourvoir définir tes objectifs qui sont clairs, réalisables et qui te correspondent, je t'invite fortement à clique ici . Pour disposer d'éléments de comparaison entre le CTO et le PEA (et aussi l'AV), c'est par ici .
Dans cet exemple, je n'ai pas pris en compte les frais relatifs aux placements… Ces frais vont également diminuer ta performance globale. Au plus ces frais seront importants, au plus ta performance en patira… Ce qui s'applique avec le PFU s'applique avec tout ce qui impactera à la baisse ton capital… Les frais relatifs aux placements dépendent de ton courtier.
Conclusion sur les intérêts composés
Et oui je n'ai pas parlé des autres merveilles du monde mais je me suis centré sur le principe des intérêts composés. Principe qui, bien utilisé, te permettra de te créer une belle pyramide de billets (C'est un indice vers l'une des sept merveilles !)
Comme l'a dit très justement Albert Einstein, comprendre ce principe te permettra de t'enrichir. Note que je n'ai pas dit, il t'enrichira mais il permettra de t'enrichir. Et oui, connaitre ce principe est une chose, disposer d'une stratégie au sein de laquelle tu vas pouvoir l'intégrer en est une autre.
Car la définition des objectifs et l'élaboration est la base de tout. Si tu ne sais pas où tu veux aller avant te de lancer, il y a de grandes chances que tu perdes à la fois ton temps et ton argent. Je te conseille donc de commencer par définir tes objectifs et ta stratégie. Pour cela, clique ici .
Cette étape réalisée, tu pourras lire nos articles afin d'avoir une meilleure vision de ce qui existe dans le monde des placements et des investissements. Je te conseille de commencer par ici .
Que ce soit car tu souhaites diversifier, ou car tu recherches des gains rapides, il y a de fortes chances que la bourse fasse partie des moyens au sein de ta stratégie financière. En bourse, il te sera utile de disposer de certaines connaissances si tu veux en tirer le meilleur de la bourse. Pour cela, j'ai placé ici les connaissances essentielles à avoir avant de commencer !
Et comme parfois les choses peuvent sembler un peu compliquée, il est toujours intéressant de disposer d'un support afin de faciliter tout cela. Tu trouveras ici des canaux de communication qui te seront fort bien utiles.
Cela en fait des ressources… car au final, le principe des intérêts composés ca marche aussi sur nous-même. Au plus tu seras formé, informé, supporté, au plus ton patrimoine saura qu'il est conduit par un pilote de confiance. Le bout du trajet, une merveille tout simplement !
